Algorithm Gossip: 合併排序法

说明

之前所介绍的排序法都是在同一个阵列中的排序，考虑今日有两笔或两笔以上的资料，它可能是不同阵列中的资料，或是不同档桉中的资料，如何为它们进行排序？

解法

可以使用合併排序法，合併排序法基本是将两笔已排序的资料合併并进行排序，如果所读入的资料尚未排序，可以先利用其它的排序方式来处理这两笔资料，然后再将排序好的这两笔资料合併。

有人问道，如果两笔资料本身就无排序顺序，何不将所有的资料读入，再一次进行排序？排序的精神是儘量利用资料已排序的部份，来加快排序的效率，小笔资料的排序较为快速，如果小笔资料排序完成之后，再合併处理时，因为两笔资料都有排序了，所有在合併排序时会比单纯读入所有的资料再一次排序来的有效率。

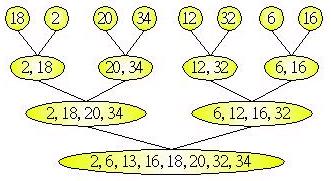
那麽可不可以直接使用合併排序法本身来处理整个排序的动作？而不动用到其它的排序方式？答桉是肯定的，只要将所有的数字不断的分为两个等分，直到最后剩一个数字为止，然后再反过来不断的合併，就如下图所示：

不过基本上分割又会花去额外的时间，不如使用其它较好的排序法来排序小笔资料，再使用合併排序来的有效率。

下面这个程式范例，我们使用快速排序法来处理小笔资料排序，然后再使用合併排序法处理合併的动作。

实作

#include <stdio.h> 
#include <stdlib.h> 
#include <time.h> 
#define MAX1 10 
#define MAX2 10 
#define SWAP(x,y) {int t; t = x; x = y; y = t;} 

int partition(int[], int, int); 
void quicksort(int[], int, int); 
void mergesort(int[], int, int[], int, int[]); 

int main(void) { 
    int number1[MAX1] = {0}; 
    int number2[MAX1] = {0}; 
    int number3[MAX1+MAX2] = {0}; 
    int i, num;  

    srand(time(NULL)); 

    printf("排序前："); 
    printf("\nnumber1[]："); 
    for(i = 0; i < MAX1; i++) { 
        number1[i] = rand() % 100; 
        printf("%d ", number1[i]); 
    } 

    printf("\nnumber2[]："); 
    for(i = 0; i < MAX2; i++) { 
        number2[i] = rand() % 100; 
        printf("%d ", number2[i]); 
    } 

    // 先排序两笔资料 
    quicksort(number1, 0, MAX1-1); 
    quicksort(number2, 0, MAX2-1); 

    printf("\n排序后："); 
    printf("\nnumber1[]："); 
    for(i = 0; i < MAX1; i++) 
        printf("%d ", number1[i]); 
    printf("\nnumber2[]："); 
    for(i = 0; i < MAX2; i++) 
        printf("%d ", number2[i]); 

    // 合併排序 
    mergesort(number1, MAX1, number2, MAX2, number3); 

    printf("\n合併后："); 
    for(i = 0; i < MAX1+MAX2; i++) 
        printf("%d ", number3[i]); 
    
    printf("\n"); 

    return 0; 
} 

int partition(int number[], int left, int right) { 
    int i, j, s; 

    s = number[right]; 
    i = left - 1; 

    for(j = left; j < right; j++) { 
        if(number[j] <= s) { 
            i++; 
            SWAP(number[i], number[j]); 
        } 
    } 

    SWAP(number[i+1], number[right]); 
    return i+1; 
} 

void quicksort(int number[], int left, int right) { 
    int q; 

    if(left < right) { 
        q = partition(number, left, right); 
        quicksort(number, left, q-1); 
        quicksort(number, q+1, right); 
    } 
} 

void mergesort(int number1[], int M, int number2[], 
                int N, int number3[]) { 
    int i = 0, j = 0, k = 0; 

    while(i < M && j < N) { 
        if(number1[i] <= number2[j]) 
            number3[k++] = number1[i++]; 
        else 
            number3[k++] = number2[j++]; 
    } 

    while(i < M) 
        number3[k++] = number1[i++]; 
    while(j < N) 
        number3[k++] = number2[j++]; 
}

Java

public class MergeSort {
    public static int[] sort(int[] number1, 
                             int[] number2) {
        int[] number3 = 
                   new int[number1.length + number2.length];
        
        int i = 0, j = 0, k = 0; 

        while(i < number1.length && j < number2.length) { 
            if(number1[i] <= number2[j]) 
                number3[k++] = number1[i++]; 
            else 
                number3[k++] = number2[j++]; 
        } 

        while(i < number1.length) 
            number3[k++] = number1[i++]; 
        while(j < number2.length) 
            number3[k++] = number2[j++];
        
        return number3;
    }
}