
解法
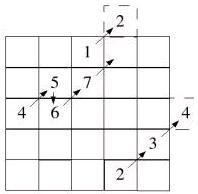
填魔术方阵的方法以奇数最为简单,第一个数字放在第一行第一列的正中央,然后向右(左)上填,如果右(左)上已有数字,则向下填,如下图所示:



#include <stdio.h>
#include <stdlib.h>
#define N 5
int main(void) {
int i, j, key;
int square[N+1][N+1] = {0};
i = 0;
j = (N+1) / 2;
for(key = 1; key <= N*N; key++) {
if((key % N) == 1)
i++;
else {
i--;
j++;
}
if(i == 0)
i = N;
if(j > N)
j = 1;
square[i][j] = key;
}
for(i = 1; i <= N; i++) {
for(j = 1; j <= N; j++)
printf("%2d ", square[i][j]);
}
return 0;
}
public class Matrix {
public static int[][] magicOdd(int n) {
int[][] square = new int[n+1][n+1];
int i = 0;
int j = (n+1) / 2;
for(int key = 1; key <= n*n; key++) {
if((key % n) == 1)
i++;
else {
i--;
j++;
}
if(i == 0)
i = n;
if(j > n)
j = 1;
square[i][j] = key;
}
int[][] matrix = new int[n][n];
for(int k = 0; k < matrix.length; k++) {
for(int l = 0; l < matrix[0].length; l++) {
matrix[k][l] = square[k+1][l+1];
}
}
return matrix;
}
public static void main(String[] args) {
int[][] magic = Matrix.magicOdd(5);
for(int k = 0; k < magic.length; k++) {
for(int l = 0; l < magic[0].length; l++) {
System.out.print(magic[k][l] + " ");
}
System.out.println();
}
}
}