Shell 排序法 - 改良的插入排序

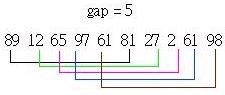
画线连结的部份表示要一起进行排序的部份，再来将间隔设定为5 / 2的商，也就是2，则第二次的插入排序对象如下所示：

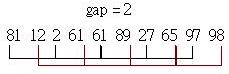
再来间隔设定为2 / 2 = 1，此时就是单纯的插入排序了，由于大部份的元素都已大致排序过了，所以最后一次的插入排序几乎没作什麽排序动作了：

将间隔设定为n / 2是D.L Shell最初所提出，在教科书中使用这个间隔比较好说明，然而Shell排序法的关键在于间隔的选定，例如Sedgewick证明选用以下的间隔可以加快Shell排序法的速度：

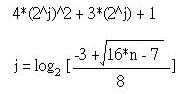
其中4*(2^j)² + 3*(2^j) + 1不可超过元素总数n值，使用上式找出j后代入4*(2^j)² + 3*(2^j) + 1求得第一个间隔，然后将2^j除以2代入求得第二个间隔，再来依此类推。

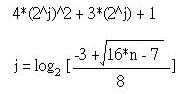
后来还有人证明有其它的间隔选定法可以将Shell排序法的速度再加快；另外Shell排序法的概念也可以用来改良气泡排序法。

实作

#include <stdio.h> 
#include <stdlib.h> 
#include <time.h> 
#define MAX 10 
#define SWAP(x,y) {int t; t = x; x = y; y = t;} 

void shellsort(int[]); 

int main(void) { 
    int number[MAX] = {0}; 
    int i;  

    srand(time(NULL)); 

    printf("排序前："); 
    for(i = 0; i < MAX; i++) { 
        number[i] = rand() % 100; 
        printf("%d ", number[i]); 
    } 

    shellsort(number); 

    return 0; 
} 

void shellsort(int number[]) { 
    int i, j, k, gap, t; 

    gap = MAX / 2; 

    while(gap > 0) { 
        for(k = 0; k < gap; k++) { 
            for(i = k+gap; i < MAX; i+=gap) { 
                for(j = i - gap; j >= k; j-=gap) { 
                    if(number[j] > number[j+gap]) { 
                        SWAP(number[j], number[j+gap]); 
                    } 
                    else 
                        break; 
                } 
            } 
        } 

        printf("\ngap = %d：", gap); 
        for(i = 0; i < MAX; i++) 
            printf("%d ", number[i]); 
        printf("\n"); 

        gap /= 2; 
    } 
}

Java

public class ShellSort {
    public static void sort(int[] number) {
        int gap = number.length / 2; 

        while(gap > 0) { 
            for(int k = 0; k < gap; k++) { 
                for(int i = k+gap; i < number.length; i+=gap) { 
                    for(int j = i - gap; j >= k; j-=gap) { 
                        if(number[j] > number[j+gap]) { 
                            swap(number, j, j+gap); 
                        } 
                        else 
                            break; 
                    } 
                } 
            } 

            gap /= 2; 
        } 
    }
    
    private static void swap(int[] number, int i, int j) {
        int t; 
        t = number[i]; 
        number[i] = number[j]; 
        number[j] = t;
    }
}

Algorithm Gossip: Shell 排序法 - 改良的插入排序

说明

解法

实作